【R】Rで対応のあるt検定を行う

今回は対応のあるt検定のRでのやり方を紹介します。

対応のあるt検定とは？

対応のあるt検定は、例えば勉強する前と後でテストの点数が異なるかどうかなど、前後比較をする場合に使われます。

2つの群の平均値に差があるかどうかを検定しているという点や、データが正規分布に従うことを前提としている点は、一般的なt検定と同じです。
対応のあるt検定が異なる点は、比較したい群の個体それぞれに対応があり、2つの群のデータがペアとして考えられるということです。

対応のあり・なしを見分けるには、同じ群の中で数値を入れ替えてもいいかどうかを考えるといいです。

具体的な例でイメージしてみましょう。
①の場合…2つの地区で生まれた赤ちゃんの平均体重に差があるか調べたい
②の場合…双子の赤ちゃんの体重に差があるかを調べたい

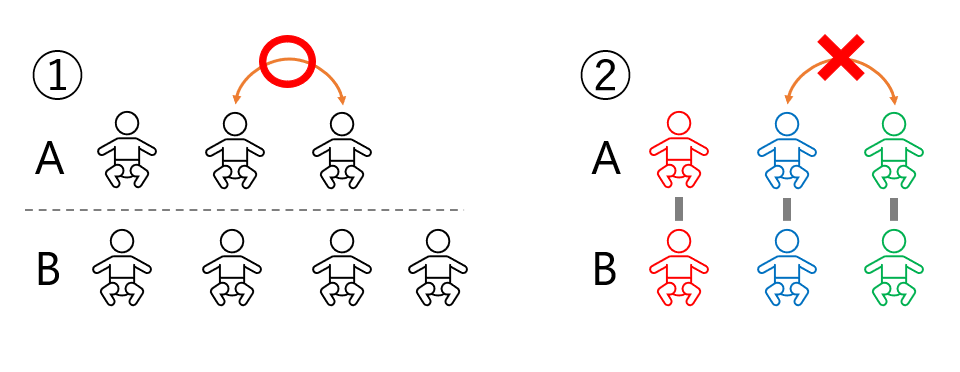
①のとき、Aの2番目の体重と3番目の体重を入れ替えても平均値の差を調べるのには問題ありません。この場合は一般のt検定を使用します。
一方、②の場合でAの2番目と3番目を入れ替えると、双子のペアが入れ替わってしまうので正しい比較ができないことになります。この場合は対応のあるt検定を使います。

また、対応のあるt検定ではペアになっているので、2つの群のデータ数は同じになります。
一方、一般的なt検定では2群のデータ数は異なっていても問題ありません。（もちろん、2群のデータ数が同じでもOKです。）

Rで対応のあるt検定

Rで対応のあるt検定を行うには
t.test(データA, データB, paired = TRUE)
と書きます。

通常のt検定に使うt.test()にオプションのpaired=TRUEを追加するだけでOKなのです。（デフォルトではpaired=FALSEになっているため、通常のt検定ではこのオプションはわざわざ記載しなくてもいいということですね。）

サンプルデータで実際にやってみましょう。

結果を見ると、p値が0.4075と表示されています。
有意水準を5%とすると、この結果は帰無仮説を棄却できず、2つの群に差があるとは言えない、と解釈できます。

以上、対応のあるt検定について紹介しました。