四分位範囲
四分位範囲とはデータの散らばりを表す指標の一つで、第一四分位(25パーセンタイル)から第三四分位(75パーセンタイル)までの長さです。
箱ひげ図の箱の部分に相当します。

IQR()で四分位範囲を求める
Rで四分位範囲を求める場合は
IQR()
と書きます。
例えば、RのサンプルデータのirisデータでPetal.Length(アヤメの花びらの長さ)の四分位範囲を求めるには
IQR(iris$Petal.Length)
となります。
|
1 2 3 |
IQR(iris$Petal.Length) [1] 3.5 |
四分位範囲が3.5であることが分かりました。
quantile()で四分位点を求める
四分位範囲だけでなく、第一四分位点(25パーセンタイル)と第三四分位点(75パーセンタイル)の値を求める方法についても見てみましょう。
箱ひげ図だと箱の端の位置に相当します。
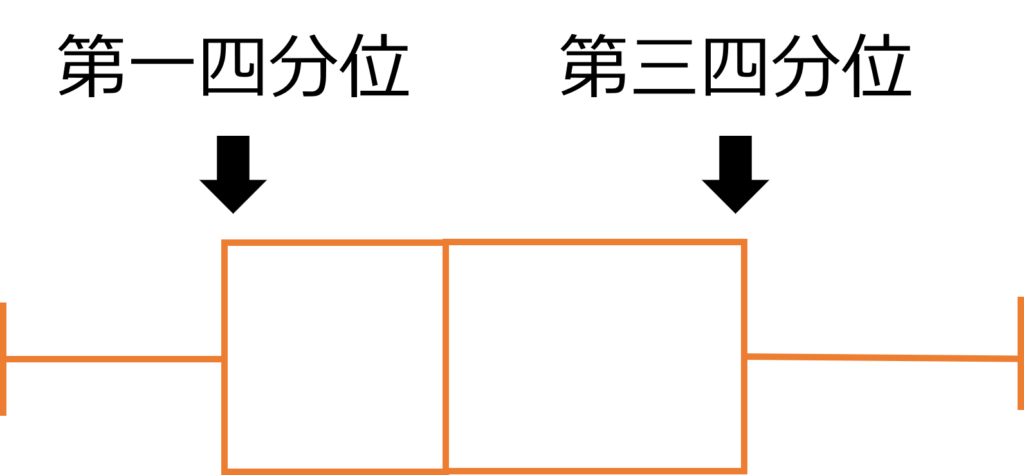
四分位点を出すには、分位点を求める関数
quantile(データ,分位点の位置)
を使うことで求めることができます。
第一四分位点は25パーセンタイルなので
quantile(データ, 0.25)
第三四分位は75パーセンタイルなので
quantile(データ, 0,75)
となります。
先ほどの例と同じくirisデータを使ってアヤメの花びらの長さで計算してみましょう。
|
1 2 3 4 5 6 7 |
quantile(iris$Petal.Length, 0.25) 25% 1.6 quantile(iris$Petal.Length, 0.75) 75% 5.1 |
第一四分位が1.6、第三四分位が5.1であることが分かりました。
最初に記載したように、四分位範囲は第一四分位から第三四分位までの長さなので、
5.1-1.6=3.5
と四分位範囲を求めることもできます。
以上、四分位範囲を求める方法を紹介しました!



コメント